High-Dimensional Data Analysis and Machine Learning

From a course by Davy Paindaveine and Nathalie Vialaneix

Camille Mondon
camille.mondon@tse-fr.eu

Toulouse School of Economics

Last updated on October 1, 2024

1 Bootstrap

Efron (1979)

1.1 Introduction

Let \(X_1, \dots, X_n \sim P_\theta\) i.i.d. Let \(\hat\theta = \hat\theta (X_1, \dots, X_n)\) be an estimator for \(\theta\).

One often wants to evaluate the variance \(\operatorname{Var} [\hat\theta]\) to quantify the uncertainty of \(\hat\theta\).

The bootstrap is a powerful, broadly applicable method:

  • to estimate the variance \(\operatorname{Var} [\hat\theta]\)
  • to estimate the bias \(\mathbb E [\hat\theta] - \theta\)
  • to construct confidence intervals for \(\theta\)
  • more generally, to estimate the distribution of \(\hat\theta\).

The method is nonparametric and can deal with small \(n\).

1.2 A motivating example

James et al. (2021)

Optimal portfolio

  • Let \(Y\) and \(Z\) be the values of two random assets and consider the portfolio: \[W_\lambda = \lambda Y + (1-\lambda) Z, \qquad \lambda \in [0,1] \] allocating a proportion \(\lambda\) of your wealth to \(Y\) and a proportion \(1-\lambda\) to \(Z\).
  • A common, risk-averse, strategy is to minimize the risk \(\operatorname{Var} [W_\lambda]\).
  • It can be shown that this risk is minimized at \[ \lambda_\text{opt} = \frac{\operatorname{Var}[Z] - \operatorname{Cov}[Y,Z]} {\operatorname{Var}[Y] + \operatorname{Var}[Z] - 2\operatorname{Cov}[Y,Z]} \]
  • But in practice, \(\operatorname{Var}[Y]\), \(\operatorname{Var}[Z]\) and \(\operatorname{Cov}[Y,Z]\) are unknown.

Sample case

Now, if historical data \(X_1=(Y_1,Z_1),\ldots,X_n=(Y_n,Z_n)\) are available, then we can estimate \(\lambda_\text{opt}\) by \[ \hat{\lambda}_\text{opt} = \frac{\widehat{\text{Var}[Y]}-\widehat{\text{Cov}[Y,Z]}}{\widehat{\text{Var}[Y]}+\widehat{\text{Var}[Z]}-2\widehat{\text{Cov}[Y,Z]}} \] where

  • \(\widehat{\text{Var}[Y]}\) is the sample variance of the \(Y_i\)’s
  • \(\widehat{\text{Var}[Z]}\) is the sample variance of the \(Z_i\)’s
  • \(\widehat{\text{Cov}[Y,Z]}\) is the sample covariance of the \(Y_i\)’s and \(Z_i\)’s.

How to estimate the accuracy of \(\hat{\lambda}_\text{opt}\)?

  • \(\dots\) i.e., its standard deviation \(\text{Std}[\hat{\lambda}_\text{opt}]\)?
  • Using the available sample, we observe \(\hat{\lambda}_\text{opt}\) only once.
  • We need further samples leading to further observations of \(\hat{\lambda}_\text{opt}\).
Figure 1: Portfolio data. For this sample, \(\hat{\lambda}_\text{opt} = 0.283\) (James et al. 2021).

Sampling from the population: infeasible

We generated 1000 samples from the population. The first three are

Figure 2: \(\color{red}{\hat{\lambda}^{(1)}_\text{opt}=0.283}\), \(\color{blue}{\hat{\lambda}^{(2)}_\text{opt}=0.357}\), \(\color{orange}{\hat{\lambda}^{(3)}_\text{opt}=0.299}\) (James et al. 2021).
  • This allows us to compute: \(\bar{\lambda}_\text{opt} = \frac{1}{1000} \sum_{i=1}^{1000} \hat{\lambda}^{(i)}_\text{opt}\)
  • Then: \(\widehat{\text{Std}[\hat{\lambda}_\text{opt}]} = \sqrt{\frac{1}{999} \sum_{i=1}^{1000} (\hat{\lambda}^{(i)}_\text{opt} - \bar{\lambda}_\text{opt})^2}\).

Here: \[ \widehat{\text{Std}[\hat{\lambda}_\text{opt}]} \approx 0.077, \qquad \bar{\lambda}_\text{opt} \approx 0.331 \ \ (\approx \lambda_\text{opt} = \frac13 = 0.333) \]

Figure 3: Histogram and boxplot of the empirical distribution of the \(\hat{\lambda}^{(i)}_\text{opt}\) (James et al. 2021).

(This could also be used to estimate quantiles of \(\hat{\lambda}_\text{opt}\).)

Sampling from the sample: the bootstrap

  • It is important to realize that this cannot be done in practice. One cannot sample from the population \(P_\theta\) since it is unknown.
  • However, one may sample instead from the empirical distribution \(P_n\) (i.e., the uniform distribution over \((X_1,\ldots,X_n)\)), that is close to \(P_\theta\) for large \(n\).
  • This means that we sample with replacement from \((X_1,\ldots,X_n)\), providing a first bootstrap sample \((X_1^{*1},\ldots,X_n^{*1})\) which allows us to evaluate \(\hat{\lambda}_\text{opt}^{*(1)}\).
  • Further generating bootstrap samples \((X_1^{*b},\ldots,X_n^{*b})\), \(b=2,\ldots,B=1000\), one can compute \[ \widehat{\text{Std}[\hat{\lambda}_\text{opt}]}^* = \sqrt{ \frac{1}{B-1} \sum_{b=1}^B ( \hat{\lambda}^{*(b)}_\text{opt} - \bar{\lambda}_\text{opt}^* )^2 } \] with \[ \bar{\lambda}_\text{opt}^* = \frac{1}{1000} \sum_{b=1}^B \hat{\lambda}^{*(b)}_\text{opt} \]

This provides \[ \widehat{\text{Std}[\hat{\lambda}_\text{opt}]}^* \approx 0.079 \]

Figure 4: Histogram and boxplot of the bootstrap distribution of \(\hat\lambda_\text{opt}\) (James et al. 2021).

(This could again be used to estimate quantiles of \(\hat{\lambda}_\text{opt}\).)

A comparison between both samplings

Results are close: \(\widehat{\text{Std}[\hat{\lambda}_\text{opt}]}\approx 0.077\) and \(\widehat{\text{Std}[\hat{\lambda}_\text{opt}]}^*\approx 0.079\).

Figure 5: Bootstrap distributions from portfolio data (James et al. 2021).

1.3 The general procedure

The bootstrap

  • Let \(X_1,\ldots,X_n\) be i.i.d \(\sim P_\theta\).
  • Let \(T=T(X_1,\ldots,X_n)\) be a statistic of interest.
  • The bootstrap allows us to say something about the distribution of \(T\): \[ \begin{array}{ccc} (X_1^{*1},\ldots,X_n^{*1}) & \leadsto & T^{*1}=T(X_1^{*1},\ldots,X_n^{*1}) \\[2mm] & \vdots & \\[2mm] (X_1^{*b},\ldots,X_n^{*b}) & \leadsto & T^{*b}=T(X_1^{*b},\ldots,X_n^{*b}) \\[2mm] & \vdots & \\[2mm] (X_1^{*B},\ldots,X_n^{*B}) & \leadsto & T^{*B}=T(X_1^{*B},\ldots,X_n^{*B}) \\[2mm] \end{array} \]
  • Under mild conditions, the empirical distribution of \((T^{*1},\ldots,T^{*B})\) provides a good approximation of the sampling distribution of \(T\) under \(P_\theta\).

Above, each bootstrap sample \((X_1^{*b},\ldots,X_n^{*b})\) is obtained by sampling (uniformly) with replacement among the original sample \((X_1,\ldots,X_n)\).

Possible uses:

  • \(\frac{1}{B-1}\sum_{b=1}^B (T^{*b}-\bar{T}^*)^2\), with \(\bar{T}^*=\frac{1}{B}\sum_{b=1}^B T^{*b}\), estimates \(\text{Var[T]}\)
  • The sample \(\alpha\)-quantile \(q^*_{\alpha}\) of \((T^{*1},\ldots,T^{*B})\) estimates \(T\)’s \(\alpha\)-quantile

Possible uses when \(T\) is an estimator of \(\theta\):

  • \((\frac{1}{B}\sum_{b=1}^B T^{*b})-T\) estimates the bias \(\mathbb E [T] - \theta\) of \(T\)
  • \([q^*_{\alpha/2},q^*_{1-(\alpha/2)}]\) is an approximate \((1-\alpha)\)-confidence interval for \(\theta\).
  • \(\ldots\)

1.4 About the implementation in R

A toy illustration

  • Let \(X_1,\ldots,X_n\) (\(n=4\)) be i.i.d \(t\)-distributed with \(6\) degrees of freedom.
  • Let \(\bar{X}=\frac{1}{n} \sum_{i=1}^n X_i\) be the sample mean.
  • How to estimate the variance of \(\bar{X}\) through the bootstrap?
n <- 4
(X <- rt(n,df=6))
[1] -0.08058779  0.28044078  1.19011050 -1.25212790
Xbar <- mean(X)
Xbar
[1] 0.0344589

Obtaining a bootstrap sample

X
[1] -0.08058779  0.28044078  1.19011050 -1.25212790
d <- sample(1:n,n,replace=TRUE)
d
[1] 2 4 4 4
Xstar <- X[d]
Xstar
[1]  0.2804408 -1.2521279 -1.2521279 -1.2521279

Generating \(B=1000\) bootstrap means

B <- 1000
Bootmeans <- vector(length = B)
for (b in (1:B)) {
  d <- sample(1:n, n, replace = TRUE)
  Bootmeans[b] <- mean(X[d])
}
Bootmeans[1:4]
[1]  0.2370868 -0.3486833  0.3521335  0.2370868

Bootstrap estimates

Bootstrap estimates of \(\mathbb E [\bar{X}]\) and \(\text{Var}[\bar{X}]\) are then given by

mean(Bootmeans)
[1] 0.03679914
var(Bootmeans)
[1] 0.1789107

The practical sessions will explore how well such estimates behave.

The boot function

A better strategy is to use the boot function from

library(boot)

The boot function takes typically 3 arguments:

  • data: the original sample
  • statistic: a user-defined function with the statistic to bootstrap
    • 1st argument: a generic sample
    • 2nd argument: a vector of indices pointing to a subsample on which the statistic is to be evaluated
  • R: the number \(B\) of bootstrap samples to consider

If the statistic is the mean, then a suitable user-defined function is

boot.mean <- function(x,d) {
  mean(x[d])
}

The bootstrap estimate of \(\text{Var}[\bar{X}]\) is then

res.boot <- boot(X,boot.mean,R=1000)
var(res.boot$t)
          [,1]
[1,] 0.1844024

2 Bagging

Breiman (1996)

2.1 Introduction

  • The bootstrap has other uses than those described above.

  • In particular, it allows us to design ensemble methods in statistical learning.

  • Bagging (Bootstrap Aggregating), which is the most famous approach in this direction, can be applied to both regression and classification.

  • Below, we mainly focus on bagging of classification trees, but it should be clear that bagging of regression trees can be performed similarly.

2.2 Classification trees

Breiman et al. (1984)

The classification problem

  • In classification, one observes \((X_i,Y_i)\), \(i=1,\ldots,n\), where
    • \(X_i\) collects the values of \(p\) predictors on individual \(i\), and
    • \(Y_i\) \(\in\{1,2,\ldots,K\}\) is the class to which individual \(i\) belongs.
  • The problem is to classify a new observation for which we only see \(x\), that is, to bet on the corresponding value \(y \in \{1,2,\ldots,K\}\).
  • A classifier is a mapping \[\begin{eqnarray*} \phi_{\mathcal{S}}: \mathcal{X} & \to & \{1,2,\ldots,K\} \\[2mm] x & \mapsto & \phi_{\mathcal{S}}(x), \end{eqnarray*}\] that is designed using the sample \(\mathcal{S}=\{(X_i,Y_i), \ i=1,\ldots,n\}\).
library(boot)
data(channing)
channing <- channing[,c("sex","entry","time","cens")]
channing[1:4,]
   sex entry time cens
1 Male   782  127    1
2 Male  1020  108    1
3 Male   856  113    1
4 Male   915   42    1

Predict sex \(\in \{\text{Male}, \text{Female} \}\) on the basis of two numerical predictors (entry, time) and a binary one (cens).

Classification trees

In Part 1 of this course, we learned about a special type of classifiers \(\phi_{\mathcal{S}}\), namely classification trees.

library(rpart)
library(rpart.plot)
fitted.tree <- rpart(sex~., data=channing, method="class")
rpart.plot(fitted.tree)

(+) Interpretability
(+) Flexibility
(–) Stability
(–) Performance

The process of averaging will reduce variability, hence, improve stability. Recall indeed that, if \(U_1,\ldots,U_n\) are uncorrelated with variance \(\sigma^2\), then \[ \text{Var}[\bar{U}]=\frac{\sigma^2}{n} \cdot \] Since unpruned trees have low bias (but high variance), this reduced variance will lead to a low value of \[ \text{MSE}=\text{Var}+(\text{Bias})^2 \] which will ensure a good performance.

How to perform this averaging?

2.3 Bagging of classification trees

Bagging

Denote as \(\phi_{\mathcal{S}}(x)\) the predicted class for predictor value \(x\) returned by the classification tree associated with sample \(\mathcal{S}=\{(X_i,Y_i), \ i=1,\ldots,n\}\).

Bagging of this tree considers predictions from \(B\) bootstrap samples \[\begin{matrix} \mathcal{S}^{*1} &=& ((X_1^{*1},Y_1^{*1}), \ldots, (X_n^{*1},Y_n^{*1})) & \leadsto & \phi_{\mathcal{S}^{*1}}(x) \\ \vdots & & & & \vdots \\ \mathcal{S}^{*b} &=& ((X_1^{*b},Y_1^{*b}), \ldots, (X_n^{*b},Y_n^{*b})) & \leadsto & \phi_{\mathcal{S}^{*b}}(x) \\ \vdots & & & & \vdots \\ \mathcal{S}^{*B} &=& ((X_1^{*B},Y_1^{*B}), \ldots, (X_n^{*B},Y_n^{*B})) & \leadsto & \phi_{\mathcal{S}^{*B}}(x) \\ \end{matrix}\] then proceeds by majority voting (i.e., the most frequently predicted class wins): \[ \phi_{\mathcal{S}}^\text{Bagging}(x) = \underset{k \in \{1, \ldots, K\}}{\operatorname{argmax}} \# \{ b:\phi_{\mathcal{S}^{*b}}(x)=k \} \]

Toy illustration: bagging with \(B=3\) trees

d=sample(1:n,n,replace=TRUE)
fitted.tree <- rpart(sex~.,data=channing[d,],method="class")
rpart.plot(fitted.tree)
predict(fitted.tree, channing[1,], type="class")

entry=782
time=127
cens=1
\(\quad \Downarrow\)
Female

d=sample(1:n,n,replace=TRUE)
fitted.tree <- rpart(sex~.,data=channing[d,],method="class")
rpart.plot(fitted.tree)
predict(fitted.tree, channing[1,], type="class")

entry=782
time=127
cens=1
\(\quad \Downarrow\)
Male

d=sample(1:n,n,replace=TRUE)
fitted.tree <- rpart(sex~.,data=channing[d,],method="class")
rpart.plot(fitted.tree)
predict(fitted.tree, channing[1,], type="class")

entry=782
time=127
cens=1
\(\quad \Downarrow\)
Male

For \(x=\,\)(entry,time,cens)\(\,=\,\)(782,127,1),

  • two (out of the \(B=3\) trees) voted for Male
  • one (out of the \(B=3\) trees) voted for Female, the bagging classifier will thus classify \(x\) into Male.

Of course, \(B\) is usually much larger (\(B=500\)? \(B=1000\)?), which requires automating the process (through, e.g., the boot function).

2.4 How much do you gain?

A simulation

We repeat \(M=1000\) times the following experiment:

  1. Split the data set into a training set (of size 300) and a test set (of size 162);
    1. train a classification tree on the training set and evaluate its test error (i.e., misclassification rate) on the test set;
    2. do the same with a bagging classifier using \(B=500\) trees.

This provides \(M=1000\) test errors for the direct (single-tree) approach, and \(M=1000\) test errors for the bagging approach.

Figure 6: Results of the simulation (Q-Q plot and boxplot).

2.5 Estimating the prediction accuracy

Estimating the prediction (lack of) accuracy

Several strategies to estimate prediction accuracy of a classifier:

(1) Compute a test error (as above): Partition the data set \(\mathcal{S}\) into a training set \(\mathcal{S}_\text{train}\) (to train the classifier) and a test set \(\mathcal{S}_\text{test}\) (on which to evaluate the misclassification rate \(e_\text{test}\)).

(2) Compute an \(L\)-fold cross-validation error:

Partition the data set \(\mathcal{S}\) into \(L\) folds \(\mathcal{S}_{\ell}\), \(\ell=1,\ldots,L\). For each \(\ell\), evaluate the test error \(e_{\text{test},\ell}\) associated with training set \(\mathcal{S}\setminus\mathcal{S}_{\ell}\) and test set \(\mathcal{S}_{\ell}\).

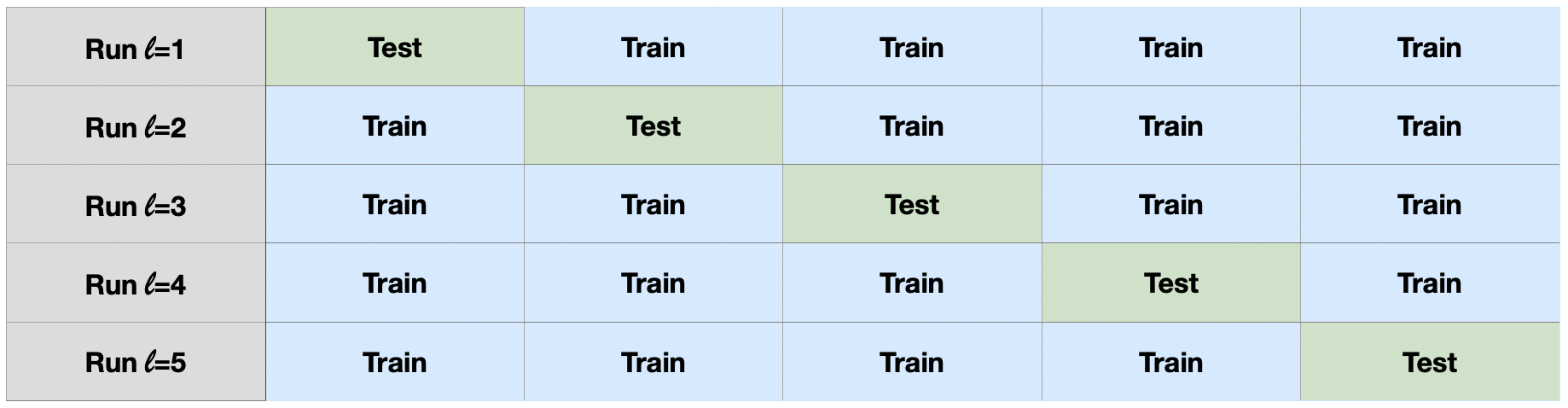
The quantity \[ e_\text{CV}=\frac{1}{L}\sum_{\ell=1}^L e_{\text{test},\ell} \] is then the (\(L\)-fold) ‘cross-validation error’.

(3) Compute the Out-Of-Bag (OOB) error1:

For each observation \(X_i\) from \(\mathcal{S}\), define the OOB prediction as \[ \phi_{\mathcal{S}}^\text{OOB}(X_i) = \underset{k\in\{1,\ldots,K\}}{\operatorname{argmax}} \# \{ b:\phi_{\mathcal{S}^{*b}}(X_i)=k \textrm{ and } (X_i,Y_i)\notin \mathcal{S}^{*b} \} \] This is a majority voting discarding, quite naturally, bootstrap samples that use \((X_i,Y_i)\) to train the classification tree. The OOB error is then the corresponding misclassification rate \[ e_\text{OOB}=\frac{1}{n}\sum_{i=1}^n \mathbb{1}[ \phi_{\mathcal{S}}^\text{OOB}(X_i) \neq Y_i] \]

Final remarks

  • Bagging of trees can also be used for regression. The only difference is that majority voting is then replaced with an averaging of individual predicted responses.
  • Bagging is a general device that applies to other types of classifiers. In particular, it can be applied to kNN classifiers (we will illustrate this in the practical sessions).
  • Bagging affects interpretability of classification trees. There are, however, solutions that intend to measure importance of the various predictors (see the next section).

3 Random forests

Ho (1995)

3.1 What can be improved?

Averaging reduces variability…

  • We argued that bagging of trees will work because averaging reduces variability: if \(U_1,\ldots,U_n\) are uncorrelated with variance \(\sigma^2\), then \[ \text{Var}[\bar{U}]=\frac{\sigma^2}{n} \cdot \]
  • However, the \(B\) trees that are ‘averaged’ in bagging are not uncorrelated! This will result into a smaller reduction of the variability.
  • Random forests have the flavour of bagging-of-trees, but they incorporate a modification that aims at decorrelating the trees.

3.2 The procedure

  • Like bagging-of-trees, random forests predict via majority voting from classification trees trained on \(B\) bootstrap samples.
  • However, whenever a split is designed in each tree, the split is only allowed among \(m(\ll p)\) predictors randomly selected out of the \(p\) predictors.
  • The rationale: in a situation where there would be one strong predictor only, most bagged trees would use this predictor in the top split, which would result in highly correlated trees. The tweak above will prevent this, hence will lead to less correlated trees.

Choosing the number of features

Using \(m=p\) would simply provide bagging-of-trees. Using \(m\) small is appropriate when there are many correlated predictors. Common practice:

  • For classification (where majority voting is used), \(m \approx \sqrt p\).
  • For regression (where tree predictions are averaged), \(m \approx \frac{p}3\).

In both cases, results are actually not very sensitive to \(m\).

Random forests

but they

3.3 A simulation

Let us look at efficiency…

We repeated \(M=1000\) times the following experiment:

  1. Split the channing data set into a training set (of size 300) and a test set (of size 162);
    1. train a classification tree on the training set and evaluate its test error (i.e., misclassification rate) on the test set;
    2. do the same with a bagging classifier using \(B=500\) trees;
    3. do the same with a random forest classifier using the randomForest function in R with default parameters (\(B=500\) trees, \(m\approx \sqrt p\)).

This provided \(M=1000\) test errors for the direct (single-tree) approach, \(M=1000\) test errors for the bagging approach, and \(M=1000\) test errors for the random forest approach.

The results

Figure 8: Comparison of single tree, bagging and random forest errors

3.4 Importance of each predictor

Measuring importance of each predictor

Because bagging-of-trees and random forests are poorly interpretable compared to classification trees, the following is useful.

The importance \(v_j\) of the \(j\)th predictor is measured as follows.

For each tree (i.e., for any \(b=1,\ldots,B\)),

  • the prediction error on OOB observations is recorded, and
  • the same is done after permuting randomly all values of the \(j\)th predictor (which essentially turns this predictor into noise), the difference between both errors is then averaged over \(b=1,\ldots,B\) (and normalized by the standard error—if it is positive), yielding \(v_j\).

(A similar measure is used for regression, based on MSEs).

Measuring importance of each predictor

Figure 9: Importance of each predictor (decreasing order)

References

Breiman, Leo. 1996. “Bagging Predictors.” Machine Learning 24 (2): 123–40. https://doi.org/10.1007/BF00058655.
Breiman, Leo, Jerome H. Friedman, Richard A. Olshen, and Charles J. Stone. 1984. Classification and Regression Trees. 1st ed. Routledge. https://doi.org/10.1201/9781315139470.
Efron, B. 1979. “Bootstrap Methods: Another Look at the Jackknife.” The Annals of Statistics 7 (1). https://doi.org/10.1214/aos/1176344552.
Ho, Tin Kam. 1995. “Random Decision Forests.” In Proceedings of 3rd International Conference on Document Analysis and Recognition, 1:278–282 vol.1. https://doi.org/10.1109/ICDAR.1995.598994.
James, Gareth, Daniela Witten, Trevor Hastie, and Robert Tibshirani. 2021. An Introduction to Statistical Learning: With Applications in r. Springer Texts in Statistics. New York, NY: Springer US. https://doi.org/10.1007/978-1-0716-1418-1.